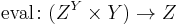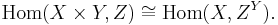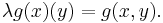Exponential object
In mathematics, specifically in category theory, an exponential object is the categorical equivalent of a function space in set theory. Categories with all finite products and exponential objects are called cartesian closed categories. An exponential object may also be called a power object or map object (but note that the term "power object" means something different in topos theory, analogous to "power set").
Contents |
Definition
Let C be a category with binary products and let Y and Z be objects of C. The exponential object ZY can be defined as a universal morphism from the functor –×Y to Z. (The functor –×Y from C to C maps objects X to X×Y and morphisms φ to φ×idY).
Explicitly, the definition is as follows. An object ZY, together with a morphism
is an exponential object if for any object X and morphism g : (X×Y) → Z there is a unique morphism
such that the following diagram commutes:
If the exponential object ZY exists for all objects Z in C, then the functor which sends Z to ZY is a right adjoint to the functor –×Y. In this case we have a natural bijection between the hom-sets
(Note: In functional programming languages, the morphism eval is often called apply, and the syntax 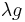 is often written curry(g). The morphism eval here must not to be confused with the eval function in some programming languages, which evaluates quoted expressions.)
is often written curry(g). The morphism eval here must not to be confused with the eval function in some programming languages, which evaluates quoted expressions.)
Examples
In the category of sets, the exponential object 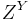 is the set of all functions from
is the set of all functions from  to
to 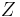 . The map
. The map 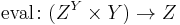 is just the evaluation map which sends the pair (f, y) to f(y). For any map
is just the evaluation map which sends the pair (f, y) to f(y). For any map 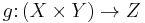 the map
the map 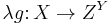 is the curried form of
is the curried form of  :
:
In the category of topological spaces, the exponential object ZY exists provided that Y is a locally compact Hausdorff space. In that case, the space ZY is the set of all continuous functions from Y to Z together with the compact-open topology. The evaluation map is the same as in the category of sets. If Y is not locally compact Hausdorff, the exponential object may not exist (the space ZY still exists, but it may fail to be an exponential object since the evaluation function need not be continuous). For this reason the category of topological spaces fails to be cartesian closed. However, the category of locally compact topological spaces is not cartesian closed either, since ZY need not be locally compact for locally compact spaces Z and Y.
References
- Adámek, Jiří; Horst Herrlich, George Strecker (2006) [1990]. Abstract and Concrete Categories (The Joy of Cats). John Wiley & Sons. http://katmat.math.uni-bremen.de/acc/.
External links
- Interactive Web page which generates examples of exponential objects and other categorical constructions. Written by Jocelyn Paine.